Despedida

Ya va terminando el curso, de modo que esta va a ser la última entrada de este blog basado en la estadística y sus aplicaciones.

 

Nunca había hecho un blog, así que esto era algo nuevo para mí. Al principio me costó arrancar (más que nada porque me echaba para atrás la idea de gastar el tiempo en algo así) pero, a medida que ha pasado el tiempo, me he acostumbrado y le he pillado el truco. También he llegado a la conclusión de que hacer un blog puede resultar muy útil, no sólo para quien lo lee, sino para quien lo hace, ya que a la vez que lo hacía he ido aprendiendo muchas cosas de la asignatura y del funcionamiento de esta página.

 

Quizás, un día de estos vuelva por aquí y haga otro blog sobre cualquier otra cosa que se me ocurra, ¿quién sabe?

 

Nada más, con esto me despido:

 

 

¡Hasta otra!

 

Seminario nº 4. Presentación del trabajo de investigación.

Poco he hablado en el blog acerca del trabajo de investigación que debemos realizar para poder aprobar la asignatura. Por ello, voy a utilizar esta entrada para explicar por encima de qué iba el trabajo de mi grupo y qué tal nos fue la presentación de éste en clase (la cual se realizó en el seminario nº 4 de la asignatura).

 

Después de varios días debatiendo el tema que íbamos a escoger, finalmente nos decidimos por hacer un estudio analítico en el que relacionamos el tener fobia a la sangre, inyecciones y heridas (SIH) con el sexo en niños y niñas de entre 10 y 14 años de un colegio de Sevilla (elegimos esta edad porque este tipo de fobia se empieza a dar sobre los 8 años aproximadamente).

 

A continuación podéis ver nuestro cronograma de trabajo:

 

 

Nos pusimos como objetivos analizar la relación entre el sexo, la edad y el curso escolar con las distintas fobias a la SIH y después de realizar los tests de hipótesis correspondientes y obtener unos resultados, llegamos a las siguientes conclusiones:

• La edad NO tiene relación con tener o no fobia a la SIH.
• El curso escolar en el que se encuentre la persona NO tiene relación con tener o no fobia a la SIH.
• El sexo NO tiene relación con tener fobia a la sangre propia, a los desmayos y a lesionarse y el dolor propio.
• El sexo SÍ tiene relación con tener fobia a los hospitales, a la sangre y el dolor ajeno y con tener fobia a las inyecciones.

 

 

En el último seminario presentamos nuestro trabajo, centrándonos sobre todo en los resultados obtenidos y la discusión de los datos. Tenemos muchas cosas que mejorar, así que para la próxima vez ya sabemos lo que tenemos que hacer, pero después de todo no nos fue demasiado mal.

 

 

Esperemos que las horas de trabajo tengan su recompensa.

 

Seminario nº 3. Análisis de datos.

En esta entrada resumiré lo que estuvimos haciendo durante el seminario nº 3, el cual nos ha servido posteriormente para saber analizar los datos de nuestro trabajo de investigación y poder plasmarlos en los resultados, la discusión de los datos y la conclusión a la que hayamos llegado con la elaboración de éste.
 

 

 

1. En primer lugar pinchamos en analizar datos y entramos en el apartado "Abrir" (read), a continuación le dimos a importar y seleccionamos nuestra vista, que en este caso recibía el nombre de "ViewOswego".
2. En el apartado de "Medias", pinchamos en "Means of" e introdujimos la variable edad "AGE" para ver que nos salía.
3. Construimos una serie de tablas de frecuencia en la que relacionamos las distintas variables (en este caso para saber con qué edad se había consumido cada alimento y saber cuál de estos alimentos provocó que la gente enfermara). En la tabla de contingencia en la que relacionamos la enfermedad con el sexo (% fila = porcentaje sobre mujeres u hombres y % columna = porcentaje sobre el nº total de enfermos) veíamos que si un recuadro destaca sobre otro, quiere decir que hay más casos en ese cuadro que destaca.
4. Por último, observamos el test de hipótesis de Chi cuadrado para saber si rechazar o aceptar la hipótesis nula del estudio. Al realizar la relación entre el helado de vainilla y la enfermedad, comprobamos que la vainilla fue el alimento que provocó el cuadro diarreico ya que existía relación estadísticamente significativa (p<0,05) entre la vainilla y la enfermedad.

 

 

Ejercicios estadística inferencial y test de hipótesis

En este caso, tuvimos que realizar otros 3 ejercicios para entregar en el campus de enseñanza virtual. Son los siguientes (en cursiva se encuentra lo que pide el problema):

1. Predeterminar el tamaño de la muestra necesaria para estudiar los niveles de glucosa plasmática de la población de una zona básica de salud. Aceptamos un riesgo de error del 1% y pretendemos una precisión de 5 mg. En una muestra reducida, la desviación típica es de 15.

2. A partir de ciertos estudios se tiene la idea de que, operando inmediatamente a enfermos que ingresan en estado de shock en un determinado servicio de un hospital, existe mayor posibilidad de que el enfermo reaccione favorablemente. Para comprobar esta hipótesis, se toman dos grupos de pacientes, a uno de los cuales se le opera inmediatamente y al otro se espera a que se recupere del estado de shock, obteniéndose los siguientes resultados:

	Recuperación completa	Mejoría	Muerte
Operado inmediatamente	10	7	3
Operado después de recuperación	5	3	2

A la vista del experimento ¿qué se puede decir respecto a la hipótesis inicial? Identifica para ello la hipótesis, las variables en estudio, el test adecuado y su resultado y conclusión final.

3. Un investigador pretende saber si las condiciones socioeconómicas influyen sobre la talla infantil. Para ello, ha obtenido la talla de 20 niños de 5 años de edad, de dos condiciones socioeconómicas contrastantes (alta y baja), que se exponen en la siguiente tabla. Plantea la hipótesis pertinente, realiza la elección del test oportuno y toma la decisión que proceda respecto a la hipótesis planteada.

 

Nivel socioeconómico bajo	Nivel socioeconómico alto	(x1- x‾1)	(x1- x‾1)2	(x2- x‾2)	(x2- x‾2)2
101	103	0.1	0.01	-2	4
102	105	11,1	1,21	0	0
100	104	-0,9	0,81	-1	1
104	106	3,1	9,61	1	1
102	108	1,1	1,21	3	9
99	100	-1,9	3,61	-5	25
102	108	1,1	1,21	3	9
103	104	2,1	4,41	-1	1
97	105	-3,9	15,21	0	0
99	107	-1,9	3,61	2	4
x‾1=100,9	x‾1=105		Σ (x1- x‾1)2 = 40,9		Σ(x2 - x‾2)2 = 54

 

Tests de hipótesis.

En el tema 10 de la asignatura hemos dado los siguientes tests de hipótesis:

Test de hipótesis de Chi Cuadrado (x²): Indica cuánto se acercan o se alejan los valores observados de los valores obtenidos. Se usa para dos variables cualitativas dicotómicas. La fórmula que se usa para calcularla es la siguiente:

Según el grado de libertad y el nivel de confianza, la significación estadística varía. En una tabla de 2x2 el grado de libertad sería 1 y si tenemos un nivel de confianza del 95%, chi cuadrado debe ser mayor que 3,84 ( x² > 3,84) para poder rechazar la hipótesis nula. Esto se puede saber mirando la tabla de valores de x² que podemos ver a continuación:

Test de hipótesis t de Student (t): Se usa para una variable cualitativa y otra cuantitativa. Si tenemos 2 grupos, usaremos la media de cada uno de ellos. La fórmula para calcula la t de Student es la siguiente:

La tabla de distribución t de Student es la que vemos a continuación:

Para saber qué valor es el que tiene que superar la t para que la hipótesis nula sea rechazada, se debe contar los grados de libertad que correspondan y saber cuál es el nivel de confianza. Por ejemplo, si tenemos 10 grados de libertad y el nivel de confianza es del 95%, el valor mínimo que debe alcanzar la t es de 1, 812 (t > 1,812) para que exista relación estadísticamente significativa y poder rechazar la hipótesis nula y aceptar la hipótesis alternativa correspondiente.

Personalmente, este tema me ha parecido sencillo. Es uno de los que mejor he entendido.

Ejercicios estadística inferencial.

Aquí os dejo tres ejercicios (con sus soluciones) que hicimos para mandar al campus virtual y posteriormente ser corregidos por el profesor:

1. Estamos interesados en conocer el consumo diario medio de cigarrillos entre los alumnos de Centros de Bachillerato de nuestra localidad. Seleccionada una muestra aleatoria de 100 alumnos se observó que fumaban una media de 8 cigarrillos diarios. Si admitimos que la varianza de dicho consumo es de 16 cigarrillos en el colectivo total, estime dicho consumo medio con un nivel de confianza del 95%.

Solución: IC (95%) = (7.22, 8.87)

2. Se desea hacer una estimación sobre la edad media de una determinada población. Calcula el tamaño de la muestra necesario para poder realizar dicha estimación con un error menor de medio año a un nivel de confianza del 99,73%. Se conoce de estudios previos que la edad media de dicha población tiene una desviación típica igual a 3.

Solución: De 324 personas, al menos, debe estar compuesta la muestra.

3. Tomada al azar, una muestra de 120 estudiantes de una Universidad, se encontró que 54 de ellos hablaban inglés. Halle, con un nivel de confianza del 95%, un intervalo de confianza para estimar la proporción de estudiantes que hablan el idioma inglés entre los estudiantes de esa Universidad.

Solución: IC (95%) = (0.36, 0.54)

 

 

Intervalo de confianza y tipos de muestreo.

Esta entrada es la continuación de la última entrada, que correspondía al tema 9. En esta ocasión voy a definir qué es el intervalo de confianza, el nivel de confianza y el muestreo, y mostraré un esquema de los tipos de muestreo que hay.

• Intervalo de confianza: Es un medio para conocer el parámetro en una población midiendo el error aleatorio. Está formado por un par de nºs entre los que se estima que estará cierto valor desconocido con una determinada probabilidad de acierto. Se calcula considerando que el estimador muestral sigue una distribución normal, como se establece en la teoría central del límite.
• Nivel de confianza: Es la probabilidad de éxito en la estimación. Se representa por 1 - alfa.

El nivel de confianza y la amplitud del intervalo varían conjuntamente. Cuanto más amplio sea un intervalo, más posibilidades de acierto (mayor nivel de confianza) habrá.

• Muestreo: Método tal que al escoger un grupo pequeño de una población podamos tener un grado de probabilidad de que ese pequeño grupo posea las características que estamos estudiando.

En el siguiente esquema podemos ver los tipos de muestreo:

 

 

 

 

Estadística inferencial: Teorema central del límite

En esta entrada he decidido poneros un video que vimos en clase acerca de una de las partes más importantes de la bioestadística. En él, trata los conceptos que dimos en el tema 9 de la asignatura, entre ellos explica el Teorema Central del Límite, una de las bases de la estadística inferencial.

Considero que se entiende bastante bien y lo explica mucho mejor de lo que lo podría hacer yo, así que aquí o lo dejo:

Distribución normal y medidas de asimetría y curtosis.

En la segunda parte del tema 8, estuvimos viendo cuál es la distribución normal que se usa en estadística.

 

La distribución de Gauss es la distribución normal que se usa como referencia, ya que es la distribución de probabilidad de variable continua que ´con más frecuencia se da en fenómenos reales. Su gráfica corresponde a la campana de Gauss:

 

 

En el punto medio de la campana se concentran la media, la mediana y la moda. El punto de inflexión corresponde con la desviación típica. Los valores de los extremos son valores aislados, que dentro de la campana representan el 0,1 %.

 

Una distribución normal sigue los siguiente principios básicos:

• Media 3 veces la desviación típica (S)= 99,73% de las observaciones.
• Media  2,58 x S = 99% de las observaciones.
• Media  2 x S = 95,45% de las observaciones.
• Media  1,96 x S = 95% de las observaciones.
• Media  1 x S = 68,26% de las observaciones.

Asimetría: Hace referencia al grado en que los datos se reparten por encima y por debajo de la tendencia central. La distribución puede ser: asimétrica hacia la izquierda (asimétrica negativa cuando As < 0), simétrica (si As = 0) o asimétrica hacia la derecha (asimétrica positiva cuando As > 0).

 

 

 

Curtosis: Hace referencia al grado de apuntamiento de una distribución.

• Si Cr > 0, la distribución es leptocúrtica.
• Si Cr = 0, la distribución es mesocúrtica.
• Si Cr < 0, la distribución es platicúrtica.

 

 

 

Medidas de tendencia central, de posición y de dispersión.

En esta nueva entrada comentaré los aspectos que para mí son más importantes de la primera parte del tema 8 de la asignatura, haciendo un pequeño resumen de éste.

 

MEDIDAS DE TENDENCIA CENTRAL: Son los valores típicos o representativos de un conjunto de datos. Me centraré en 3 de ellas:

• Media (media aritmética): Es el centro de gravedad de nuestros datos y se calcula para variables cuantitativas. Considera todos los valores de la variable.

• Mediana (Me): Es el punto para el que la distancia media a los valores de la muestra es mínima. Se calcula para variables cuantitativas. Sólo tiene en cuenta la posición de los valores en la muestra. Si hay más de una mediada, se toma el punto medio entre la mediana mayor y la más pequeña.
• Moda (Mo): Es el valor con mayor frecuencia, es decir, el que se repite más veces. Si hay más de una se dice que la variable es multimodal. Se calcula para cualquier tipo de variable.

 

MEDIDAS DE POSICIÓN: Se calculan para variables cuantitativas y sólo tienen en cuenta la posición de los valores en la muestra. Son los llamados "cuantiles" y pueden ser:

• Cuartiles: Ordenan la muestra en 4 partes:
• Q1 (primer cuartil): al menos el 25% de los datos son menores o iguales que él.
• Q2 (segundo cuartil): al menos 50% de los datos menos o iguales que él (corresponde a la mediana).
• Q3 (tercer cuartil): al menos el 75% de los datos son menores o iguales que él.
• Q4 (cuarto cuartil): es el mayor valor que se alcanza en la muestra.
• Deciles: Dividen la muestra ordenada en 10 partes.
• Percentiles: Ordenan la muestra en 100 partes. En este caso, Q1 = P25 y Q3 = P75.

 

MEDIDAS DE DISPERSIÓN: Se usan para variables cuantitativas y se definen para variables no agrupadas. Hablaré de 3 de ellas:

• Rango o recorrido (R): Es la diferencia entre el mayor y el menor valor de la muestra.
• Desviación típica (S): Cuantifica el error que cometemos si representamos una muestra únicamente por su media.
• Varianza muestral: Desviación típica al cuadrado.

 

 

Y esto es todo. Próximamente me centraré en la segunda parte de este tema 8.

 

(A partir de ahora publicaré las entradas más seguidas, ya que el plazo que tenemos para hacer el blog es hasta el 14 de Junio).

Representaciones gráficas.

Para hacer esta entrada voy a basarme en la segunda parte del tema 7, en la que vimos como se pueden representar los datos a través de gráficas. Así que para ello, voy a explicar y a enseñaros los tipos de gráficas que más se usan normalmente:

• DIAGRAMA DE BARRAS: En el eje OX se representan los valores de las variables levantando una barra longitudinal que es igual a la frecuencia relativa.

 

• PICTOGRAMA: Figuras cuya área es la frecuencia del valor que representan.

 

• GRÁFICO DE SECTORES: Se divide un círculo en sectores proporcionales a la frecuencia relativa de un valor.

 

• HISTOGRAMA (representación más frecuente con datos agrupados): Está formado por un grupo de rectángulos cuyas bases coinciden con el intervalo que representan y cuyos valores aparecen en el eje OX (el área del rectángulo debe ser igual a la frecuencia relativa del intervalo).

 

• POLÍGONO DE FRECUENCIAS: Se obtiene uniendo los puntos medios de los extremos superiores de los rectángulos que forman el histograma.

 

• DIAGRAMA DE TRONCO O TALLO Y HOJAS: Si los datos son 2 dígitos, a la izquierda (en el tronco o tallo) aparece la cifra de las decenas, a la derecha separadas por una línea aparecen las hojas y se escriben todas seguidas. Si hay 3 dígitos el tallo está formado por los dos primeros.

 

 

Considero que la parte de la representación de datos es la más "divertida" de todo el proceso que se lleva a cabo cuando se realiza un estudio y se obtienen los resultados de éste.

 

 

Estadística y tipos de variables.

Con esta entrada, lo que pretendo es que quede claro el concepto de estadística y los tipos de variables que existen y que podemos usar en el estudio que queramos realizar. Para ello me voy a centrar en lo que vimos en la primera parte del tema 7 de la asignatura.

ESTADÍSTICA: Cuerpo de conocimientos para aprender de la experiencia y poner en números las respuestas de las personas para poder relacionarlas. Según la RAE, se define en una de las acepciones como "estudio de los datos cuantitativos de la población, de los recursos naturales e industriales, del tráfico o de cualquier otra manifestación de las sociedades humanas", otra acepción la define como "rama de las matemáticas que utiliza grandes conjuntos de datos numéricos para obtener inferencias basadas en el cálculo de probabilidades".

 

VARIABLE: Magnitud cuyos valores están determinados por las leyes de la probabilidad, como los puntos resultantes de la tirada de un dado (def. RAE). Hay dos tipos:



 

La etapa empírica de la investigación

Antes del examen parcial vimos los temas 6 y 7, de los cuales hablaré en esta entrada y en las siguientes que haga próximamente.

El tema 6 es un tema muy amplio. En él dimos, la clasificación de estudios, el algoritmo de clasificación de estudios analíticos y las medidas de frecuencia.

En esta entrada me voy a centrar sobre todo en la clasificación de estudio y las medidas de frecuencia.


CLASIFICACIÓN DE ESTUDIOS SEGÚN:

 

 

 

MEDIDAS DE FRECUENCIA:

• Prevalencia: Proporción de población que ya tiene "enfermedad" en un punto específico en el tiempo. Adopta valores en 0 y 1. La magnitud de asociación que le corresponde es la razón de prevalencia, que relaciona la prevalencia de los expuestos y los no expuestos.
• Incidencia: Describe la frecuencia de nuevos casos que ocurre durante un período de tiempo. La magnitud de asociación de ésta es el riesgo relativo (razón de incidencia), que mide la relación entre los expuestos y los no expuestos.
• Odds ratio: Se usa en el estudio de casos y controles y la población ya está "enferma". Mide la relación entre la razón de los casos y la razón de los no casos.

 

A la hora de llegar a una conclusión, hay que tener en cuenta lo siguiente:

• Si la razón de prevalencia (RP) o el riesgo relativo (RR) da como resultado 1 (RP o RR = 1), no hay asociación, por lo que se da por válida la hipótesis nula (h₀).
• Si RP o RR < 1, se rechaza la h₀ y se acepta una de las hipótesis alternativas.
• Si RP o RR = 0 (o muy próxima), hay más enfermos entre los no expuestos que entre los expuestos.
• Si RP o RR > 1, se rechaza la h₀ y se acepta la otra hipótesis alternativas.

 

Seminario nº 2. Tablas de frecuencia y gráficos.

En el segundo seminario de la asignatura nos centramos en la pestaña "Analiza datos" de Epi Info.

 

Para realizar el análisis pinchamos en el "abrir", que se encuentra en el apartado de "datos" a la izquierda de la imagen, y seleccionamos la vista "ViewOswego"

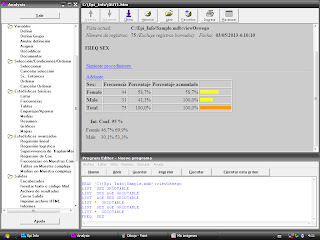
Una vez hecho esto, nos sale que el nº de registros es 75, es decir, que tenemos 75 personas registradas que completaron el cuestionario realizado en el seminario anterior.
El paso siguiente sería relacionar las edades de las personas con el sexo. Para ello pichamos en "estadística básica" y entramos en "listar". Si marcamos "todo menos" y no seleccionamos nada, nos saldría todo el listado.

 

Para hacer una tabla de frecuencias le damos al apartado de "frecuencias" y ponemos, en este caso, la palabra "SEX" en "frecuencia de" y hacemos otra con la palabra "ILL".

 

 

 

En este caso el intervalo de confianza es del 95%. Este intervalo es un estimador poblacional y si es muy amplio nos indica que tenemos una muestra muy dispersa.

 

A continuación procedemos a agrupar las variable para convertir la variable cuantitativa en cualitativa. Tomamos 3 intervalos según el grupo de edad. Pinchamos en "definir" en el apartado de "variables" y nos sale el siguiente cuadro, que completaremos.

Seguidamente le daremos a "recodificar" y crearemos los grupos de edad correspondientes:

1. Menores de edad: 0-17
2. Adultos: 18-65
3. Ancianos: 66-120

 

 

Realizamos una tabla de frecuencia con estos datos: 

 

 

 

Seguidamente entramos en el apartado de "gráficos", elegimos "sexo" como variable principal para hacer un gráfico de sectores en el que se vea reflejado la cantidad de hombres y mujeres (imagen 1) y hacemos un histograma para ver la variable "edad" (imagen 2).

Imagen 1.

Imagen 2.

El siguiente paso sería realizar un gráfico (imagen 3) relacionando los diferentes alimentos consumidos en la fiesta del caso que estamos analizando y la cantidad de personas los consumieron o no (contestaron "sí" o "no").

Imagen 3.

 



Es conveniente saber que las imágenes de los gráficos que hagamos con este programa se guardan automáticamente en el ordenador.

Pienso que lo bueno de este tipo de seminarios es que nos servirán mucho (o eso espero) para el trabajo de investigación que seguimos realizando.